Parallel and Perpendicular Lines
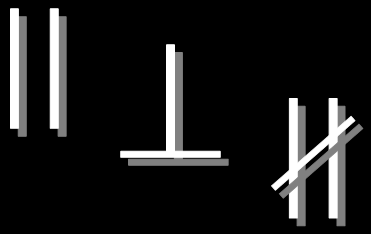
When we talk about something being parallel, it means there are two lines that are going in the same direction, the same distance apart.
To be exact, this relationship must be true always – no matter how long the lines are, these lines must not ever, ever, ever, ever, ever, ever cross. That can only happen if they are exactly straight and they are always exactly the same distance apart.
It is hard to find exact parallel in nature (we should just say parallel since ‘exact’ parallel is redundant if we follow the strict definition of parallel) – and it is hard to manually build parallel pieces of most things for very long segments.
Being parallel seems like a steep challenge, but when it happens – or when you want to represent the condition – it earns the symbol for Parallel:

Otherwise, is gets the symbol for Not Parallel:

Perpendicular, on the other hand, is exactly as far away from being parallel as you can get. This is when the angle of one line to another is exactly 90 degrees. This is called a ‘right angle’ and, for some reason, this condition is also called ‘normal’ – as in line A being normal to line B – (which is a little strange seeing as how it is really hard to get something exactly 90 degrees… try building something square and see if you can make all four pieces line up exactly with 90 degree angles). We show this relationship with the symbol for Perpendicular:

Or on a drawing, the symbol for a right angle is shown by a little box in the corner of the angle that is 90 degrees:

In math, these relationships are used frequently in calculations. See the triangle page to learn how to determine the area of a triangle and for calculating the unknown side of a right triangle – both are based on having 90 degree angles.
Click here for a free downloadable practice sheet! Parallel and Perpendicular Lines Worksheet

Pingback: Parallel and Perpendicular Lines Practice - Math Games for kids