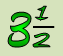Basic Fractions, Improper Fractions, Mixed Numbers, Decimals, Percentage

Fractions are used to show partial amounts of whole numbers.
If, for example, we have a value more than 1, but less than 2, we can use fractions to show the exact amount (or a very close approximation).
There are three parts to a fraction: the numerator, the fraction bar, and the denominator. The numerator is the number of equal parts or pieces you have and the denominator is the size of the pieces or divisions. The numerator and the denominator are separated by the line, or fraction bar.
We talk about fractions by saying the numerator then the denominator with a “th” or “ths” added to the end. 5/6 is said “five sixths” (the exceptions are when a 1, 2, or 3 is at the end of the denominator, and we say ‘firsts’ and ‘half’ or ‘halves’ and ‘third’ or ‘thirds’ for them). We can also say the numerator value “over” or “out of” the denominator value, such as “five over six” or “five out of six” to give different context to the same value.
The denominator cannot be 0. This is called “undefined” as you can’t have any number of “zero-ths” and have a real value. The denominator can be 1 – and it actually is 1 for all whole numbers, we just choose to not write it. For example, the fraction 7/1 is the same as 7. We have 7 “oneths”.
To have 5/6 means that we have 5 pieces, each a sixth in size. The sixth is one piece of a ‘whole unit’ divided into 6 equal parts and 5/6 means that we have 5 of those divisions. Think of a pie divided into 6 equal pieces. The entire pie has 6 sixths, or 6/6. Remove a piece, and there are 5 left, or 5/6. The original, uncut pie is a whole pie – or 1. If it is divided into 6 pieces, all the same size, the whole pie is equal to 6/6. Any time the numerator equals the denominator, we know the value is 1.
Improper Fractions
It is certainly possible to have more pieces of the division than are needed to make a whole unit. Imagine we have two pies, one has 5 of 6 pieces left and the other has 2 of 6 pieces left. If we put them together would we have an amount more than 1 full pie? Sure. We can add the 5 pieces and the 2 pieces and know that we have 7 in total. This is 7 pieces of a sixth of pie, or 7/6. When you have a numerator greater than the denominator, this is called an improper fraction and despite its name, it is a real value and has real meaning.
Mixed Numbers
Suppose that we don’t want to talk about the pie as a total count of the pieces and we need to know how many full pies we have. We can convert the 7/6 from the two partial pies above by dividing the top by the bottom and determining how many times the denominator is in the numerator. The example of 7/6 is a simple one. There is one 6 in the 7, with a remainder of 1. So to create the mixed number, or the number that includes the count of the wholes and the remaining fraction, take the result of the full division, 1, and then the remainder of the division “over” the size of the pieces (denominator). This produces the mixed number of 1 1/6, pronounced “one and one sixth”. We have 1 whole pie and 1/6 of another.
Mixed numbers to Improper Fractions
Sometimes we know how many whole numbers we have, and a leftover fraction amount (as we see in the mixed number above) but we want to know the improper fraction. This is often true when doing arithmetic with the fractions. It is easier to do the math if you know the total number of fractional pieces as written in an improper fraction. To convert a mixed number to an improper fraction, multiply the denominator by the whole number and then add the numerator. For the fraction 3 1/2, this would be 2 x 3 = 6, then 6 + 1 = 7. Make this result the numerator and put it in fraction form with the original denominator – this is the improper fraction 7/2 and it is equal to 3 1/2. The mixed number says that we have 3 wholes of 2 halves per whole, 3 x 2 = 6 halves, with the additional 1/2, we have 7 halves, or 7/2. This process works with any mixed number.
Fractions and their Decimal Values
Sometimes it is convenient to talk about the value of a partial amount using the fraction terminology and sometimes, like in calculations, we need to know the exact decimal value of the fraction. When talking about fractions, instead of saying “over” we can also use the words “divided by”. This language helps to show how the fraction also represents a decimal number. It also tells us exactly how to get that decimal number. To get the decimal value of 5/6, we take “five divided by six” and get .8333 (the 3 repeats forever…). This is the decimal value of “five sixths”. If you apply the same method to improper fractions, you will get a whole number greater than 1, with a decimal value following the decimal point.
Percentages
Many times it is clearer to talk about a partial value in terms of a percentage. Think of percent as a ratio, or relationship, between the part and the whole. Going back to the pie, we have 5/6 of the pie. What percent is this? To calculate this, the first step is to find the decimal value of the fraction, which is .8333 for 5/6. We convert this value to percent by multiplying by 100%. Think of the % as a unit, and multiply the .8333 by 100. Moving the decimal two places gives us 83.33, and adding the units of percent (%), we have 83.33%. This is the percentage representation of the fraction 5/6. They are the same, but have different uses in different places.